A resistor ladder is a brilliant but super simple way to attach multiple buttons to a single analog to digital converter (ADC) pin on an Arduino or other microcontroller. By expanding on the concept of the voltage divider, the resistor ladder offers a way to create various reference voltages by tapping into each ‘rung’ of the ladder. Consider the following schematic:
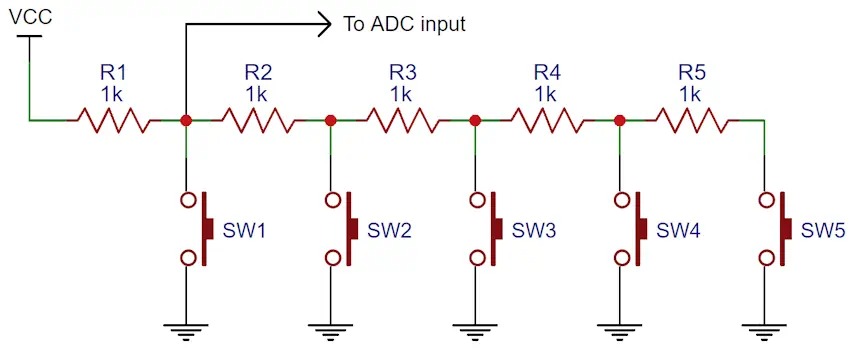
By attaching our analog pin between the first and subsequent series resistors and a button to earth at each ‘rung’, we’re effectively creating a variable voltage divider. If we measure or calculate the values read by our analog pin, we can interpret each reading as a different button being pressed with a few lines of code:
#define INPUT_PIN A0 void setup() { Serial.begin(9600); pinMode(INPUT_PIN, INPUT); } void loop() { int result = readAnalogButton(); Serial.println(result); } int readAnalogButton() { int button = analogRead(INPUT_PIN); if (button > 921) return 0; if (button < 256) return 1; if (button < 598) return 2; if (button < 726) return 3; if (button < 794) return 4; if (button < 921) return 5; }
Rather than telling our code to look for the exact values we expect the analog pin to read, we set a range of values that can be interpreted as belonging to a specific button. We do this by calculating the points halfway between each expected ADC reading and set these as as the boundaries of our ranges. Just like that, we’ve got 5 buttons on the one pin! We’re not done just yet though, because this is just about the worst possible way we could implement this.
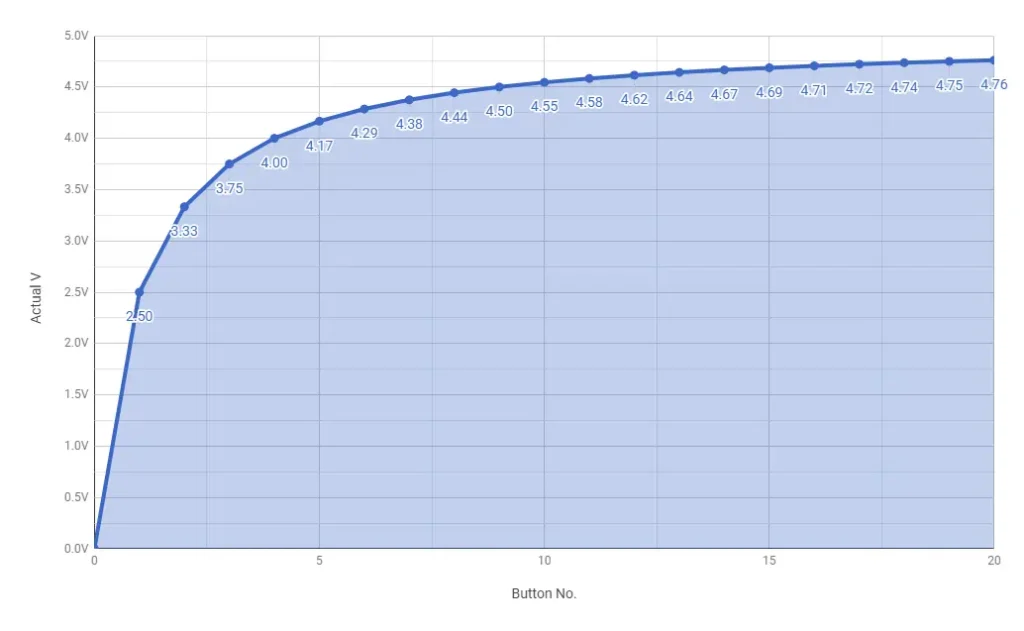
Assuming perfect resistors, the voltage readings for each button should be around 0.0V, 2.5V, 3.33V, 3.75V and 4.0V, with corresponding ADC readings of around 0, 512, 683, 768 and 819. You might have already noticed a trend by this point…
If we add another 5 switches each with a 1kΩ resistor, the subsequent voltages will be 4.17V, 4.29V, 4.38V, 4.44V and 4.5V, and will continue to grow logarithmically with each 1kΩ resistor we add:
This might work for a project with a small number of buttons if you measure each value, and calculate and hard-code your ADC boundaries for each button – but magic numbers are bad, and you should feel bad.
If we change the voltage scaling from logarithmic to linear, each adjacent ADC value will become roughly equidistant. This means that we can dynamically calculate the corresponding button for any given reading, rather than hard-coding fixed values. This allows us to use the same piece of code for any number of buttons and as a bonus, uses the full range of our ADC – in the above example, we jump straight from 0 to 512 between the first two buttons – that’s half our resolution!
So, how do we know what resistors we should use?
For the following example, I’ve used a 47k Ω resistor for R1. I’ve chosen this value as it allows us to operate the circuit at a super low current (by Ohm’s law, 5V / 47kΩ = 0.11 mA) and still use a wide-range of commonly available resistor values. We’ll use 5 buttons total, and calculate the value for button 1 (which is actually the second button, like a zero-indexed array).
Since we have a fixed value of R1 we can work out the value for R2 using the following formula:
Rbutton = R1 / (1 – (Bindex / Btotal)) – Rtotal
Where Bindex is the index of the button in question, Btotal is the total number of buttons and Rtotal is the combined value of all resistors in the circuit prior to the current (in this case, it’s just the 47kΩ for button 0). So from the above, we have 47000 / (1 – (1 / 5)) – 47000 = 11750Ω. We can use a lookup table to find our closest equivalent value, which in this instance is 12kΩ.
If we do this for the remaining buttons, we get values of 20k, 29k and 120k, which should give us corresponding ADC readings of around 0, 208, 415, 616 and 822.
That’s still a bit of a process to work out – especially if you’ve got more than a handful of buttons, which is why I made this Google Sheets spreadsheet to do all the heavy lifting! Please note you’ll need to make a copy of this if you want to edit it and use your own values. Just enter the number of buttons you want to use and the tolerance of your resistors (which is only a consideration with a very large number of buttons – otherwise you can leave this at the default 2%.)

The column you’re most interested in is “Closest R” – this performs a lookup of the closest common resistor value to the calculated required value. The “Req’d” columns indicate the exact values we’re looking for, while the “Actual” columns indicate the voltages for the calculated closest available resistor. “Variance” simply tells us the difference between the current and previous ADC reading – if the result here is greater than the specified resistor tolerance, this will be indicated by the “In Tolerance” column.
Great – so we’ve got our resistors all worked out – all that’s left now is the code!
#define BUTTONS 5 #define RESOLUTION 1023 int readAnalogButton() { float avg = RESOLUTION / float(BUTTONS); int val = analogRead(ANALOG_PIN); if (val > (BUTTONS - 0.5) * avg) { return 0; } for (int i = 0; i < BUTTONS; i++) { if (val < round((i + 0.5) * avg)) { return i + 1; } } return 0; }
We start by determining the average difference between adjacent ADC readings, enabling us to dynamically calculate each button’s expected ADC reading. To test for an open circuit – the most likely result – we check if the measured value is less than halfway between 0 and our dynamically-calculated reading for the first button. If this evaluates to false, we begin by testing for each button in turn, comparing our ADC reading against the range boundaries that lie between adjacent readings, until we find a match.
Note that because “no button pressed” is a valid result in addition to each individual button press, we treat a zero value as an open circuit, and commence indexing our buttons from 1, as opposed to the zero index used during calculation.
With the above code, we can scale up and down by simply changing the value defined by the macro #define BUTTON 5 , with the number of buttons only limited by the tolerance of your resistors and resolution of your microcontroller’s ADC. We’ll see just how far we can push this in a future post!
If I use 3,3v how modify the spreadsheet?
Thank you , Simon
Hi Simon, sorry I'm late to respond here!
I've modified the spreadsheet so you can enter the voltage yourself – thanks for the feedback! I should recognise that not all ADCs reference 5V – the ESP8266 references only 1V, for example!
You'll need to make a copy of this file to your own Google Drive using the "Make a copy" function from the "File" menu. This will make a copy that you're free to edit and play with as much as you like!
Good luck – let me know if you need any further help with it.
Thanks for this post!
Awesome information once again! I am looking forward for your next post:)
if we press two or more keys in that case adc will interpret the different adc value and different key function will execute.
am i right?
Hi sdev!
You've discovered the limitation of this particular implementation!
Because electricity will always follow the path of least resistance (no pun intended!) it will only ever register the lowest button push, no matter how many buttons you've got or are holding down.
It's certainly not a perfect solution, but definitely a handy one for when you don't need to read more than one button press. If you want to look at an option that will allow this with minimal GPIOs, take a look into multiplexing.
Thanks for stopping by! 🙂
Thanks for such a great article! I am building the water sensor (https://create.arduino.cc/projecthub/Pedro52/arduino-esp32-diy-water-level-sensor-and-diy-level-indicator-3d513d) and turning it into a remote-controlled sump pump controller. I used your idea to get it working, but I had some trouble. First, I used resistors that I had on hand, and the spreadsheet said the tolerance was ok. But the values didn't land correctly with the sample code. I had to dramatically increase the tolerance. Here is my output (the code would set the switch number on the second-to-last line beginning with Average…):
LEVELarray: 0 = 0 Analog value: 942 Level: 0
Average:204.80 val: 185 round((i + 0.92) * avg): 188.00 i: 0 BUTTONS: 5
LEVELarray: 1 = 80 Analog value: 185 Level: 1
Average:204.80 val: 353 round((i + 0.92) * avg): 188.00 i: 0 BUTTONS: 5
Average:204.80 val: 353 round((i + 0.92) * avg): 393.00 i: 1 BUTTONS: 5
LEVELarray: 2 = 119 Analog value: 353 Level: 2
Average:204.80 val: 505 round((i + 0.92) * avg): 188.00 i: 0 BUTTONS: 5
Average:204.80 val: 505 round((i + 0.92) * avg): 393.00 i: 1 BUTTONS: 5
Average:204.80 val: 505 round((i + 0.92) * avg): 598.00 i: 2 BUTTONS: 5
LEVELarray: 3 = 1 Analog value: 505 Level: 3
Average:204.80 val: 655 round((i + 0.92) * avg): 188.00 i: 0 BUTTONS: 5
Average:204.80 val: 655 round((i + 0.92) * avg): 393.00 i: 1 BUTTONS: 5
Average:204.80 val: 655 round((i + 0.92) * avg): 598.00 i: 2 BUTTONS: 5
Average:204.80 val: 655 round((i + 0.92) * avg): 803.00 i: 3 BUTTONS: 5
LEVELarray: 4 = 0 Analog value: 655 Level: 4
Average:204.80 val: 807 round((i + 0.92) * avg): 188.00 i: 0 BUTTONS: 5
Average:204.80 val: 807 round((i + 0.92) * avg): 393.00 i: 1 BUTTONS: 5
Average:204.80 val: 807 round((i + 0.92) * avg): 598.00 i: 2 BUTTONS: 5
Average:204.80 val: 807 round((i + 0.92) * avg): 803.00 i: 3 BUTTONS: 5
Average:204.80 val: 807 round((i + 0.92) * avg): 1008.00 i: 4 BUTTONS: 5
LEVELarray: 5 = 0 Analog value: 807 Level: 5
Hi – thanks for your input!
If you've used resistors that you've got on hand, then I'm afraid the code may not work as expected – however you might get lucky!
How many resistors are in your ladder (and what values did you have on hand?) Let's work through it, as I'm always keen to see other implementations!
– Chris.
Correction: the code would set the switch number on the last line…
I realized that once I extend wires into my sump pit, all the resistances go out the window.
https://docs.google.com/spreadsheets/d/1Ye5LhEKRTZ23IbOV4acUScxaAs0CzQEXB9rr6Fg8PCQ/edit?usp=sharing
See the manually entered actual resistor values. Also see by reply to my comment.
Thanks for the quick reply.
I am using resistor ladders on my model railway control panels. I wire the buttons in groups of 8 as 8 bits make a byte which is handy for controlling things over the i2c buss.i carefully select the resistor values to give analogRead values or 50,150,250,350,450,550,650 and 750. Therefor int pinNumber = analogRead pin/100 returns a number between 0 and 7 which can be used in switch/case etc.
This is just what I'm looking for — thank you!
it helped me solve my problem with 3 wires and 12 button supper
If you're pressing SW1 then it's impossible to know whether any other switches are being pressed…
You're absolutely correct – another commenter earlier has pointed out the same. It's a limitation of what is at the end of the day a very basic implementation.
Because electricity will always follow the path of least resistance (no pun intended!) it will only ever register the lowest button push, no matter how many buttons you've got or are holding down.
It's certainly not a perfect solution, but definitely a handy one for when you don't need to read more than one button press. If you want to look at an option that will allow this with minimal GPIOs, take a look into multiplexing.
thanks for this article. I purchased one of these Analog Button Keyboards off Amazon and found the buttons to be noisy. Both in terms of the value returned by the analogRead() as well as the time it took to reach a stable state. On the way up I would get values that my code interpreted as other precesses. So I created some debounce and error correction logic around my button states.
Which could also be noise introduced by my breadboard.(I didn't have a good way to determine that.)
Hello. I am currently trying to use this method for a circuit simulation. The arduino uno always returns 0 as the value and the analog pin reads 1023 all the time.
I have nine buttons.
Hi, I'm confused by the example: You have 5v and 5 switches, R1 = 1k, then R2,R3,R4,R5 are 1k resistors too. Your spreadsheet – shows 5x rows for "Closest R": 47000,12000,20000,39000,120000
Do you just repeat the 12000 resistor for all steps, as in your example, or should the resistors change on each step?
I am trying to do 3.3v with 4 switches. Am I correct this would be 3 steps of "closest R": 16000, or 5Ω
Many thanks.
I'm getting an off by one error, and I'm not sure what is causing it.
I'm building a circuit with 16 switches (Arduino Nano, ADC res 1023, 5v). I set the spreadsheet to 16 switches, and built the circuit with the recommended resistor values. I measured values, and plotted them against the expected values, and the measured values had a steeper slope than expected (measured values went from 0 to 1023, instead of the expected 0 to 960). The ADC measured the same value whether the last switch was open or closed.
If I set the spreadsheet to 17 switches, and built the circuit using the recommended resistor values (but left out the last resistor, and only used 16 switches), then the measured slope matched the expected values for a 16 switch ladder (0 to 960).